[게임수학] 수
수와 집합
|
분류
|
정의
|
기호
|
예
|
|
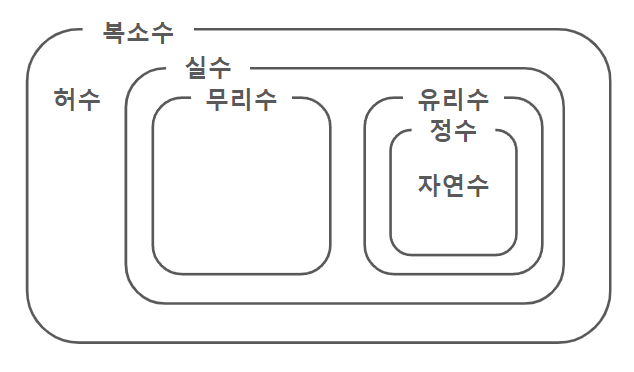
자연수
|
물건을 세거나 순서를 지정하기 위해 사용하는 수의 집합
|
ℕ
|
1,2,3
|
|
정수
|
자연수와 자연수의 음수 0을 포함하는 수의 집합
|
ℤ
|
-1,0,1
|
|
유리수
|
분모가 0이 아닌 두 정수의 비율 혹은 분수로 나타낼 수 있는 수의 집합
|
ℚ
|
½, ⅞
|
|
무리수
|
두 정수 비 혹은 분수로 나타낼 수 없는 수의 집합
|
𝕀
|
sqrt2, π
|
|
실수
|
유리수와 무리수를 포함하는 수의 집합
|
ℝ
|
위에 다
|
|
복소수
|
실수와 제곱하면 -1이 되는 허수 단위 i를 조합해
a + bi(a,b는 실수)형태로 표현하는 수의 집합
|
ℂ
|
|
|
사원수
|
실수와 제곱하면 -1이 되는 세 허수 단위 i,j,k를 조합해 a+bi+cj_dk(a,b,c,d는 실수)형탸로 표현하는 수의 집합
|
ℍ
|
|
연산과 수의 구조
수 집합의 고유한 특징은 원소를 이용해 연산을 한다는 점이다. 대표적인 연산으로는 덧셈, 뺄셈, 나눗셈, 곱셈과 같은 사칙연산이 있으며 이들은 두개의 원소를 사용해 새로운 원소를 만들어내기 때문에 이항연산이라고 부른다.
이항 연산

교환법칙, 결합법칙, 분배법칙의 3가지 성질을 가지며 항등원과 역원을 지닌다. 그리고 같은 집합에 속한 두 수를 투입한 이항연산의 결과는 항상 그 집합에 속하는 성질로 닫혀 있음 이라고 할수 있다.
교환법칙 : 두 원소의 좌우 순서를 바꿔도 결과가 동일한 성질
ex) a + b = b + a , a * b = b * a
결합법칙 : 세 원소의 연산 순서를 바꿔도 결과가 동일한 성질
ex) (a + b) + c = a + (b + c) , (a * b) * c = a * (b * c)
분배법칙 : 좌분배법칙 / a * (b + c) = a * b + a * c
우분배법칙 / (b + c) * a = b * a + c * a
항등원 : 임의의 수와 연산 결과를 항상 동일한 수로 만들어주는 수
ex) a + 0 = a 즉, 0은 덧셈의 항등원 / a * 1 = a 즉, 1은 곱셈의 항등원
역원 : 임의의 수와 연산 결과가 항상 항등원으로 만들어주는 수
ex) a + (-a) = 0 즉, -a는 a의 덧셈의 역원 / a * 1/a = 1 즉, 1/a는 a의 곱셈의 역원
닫혀있음 : 어떤 집합에서 두 원소를 사용한 이항연산의 결과가 항상 그 집합에 속하는 성질
ex) 1(자연수) + 3(자연수) = 4(자연수)
수의 표현 방법
수직선
실수를 대응시켜 시각적으로 표현한 직선이다.



방향의 속성을 부호를 통해 나타낼수 있으며 속성은 원점으로 부터의 거리를 의미한다. 그리고 이 원점으로 부터의 거리는 |ℝ|로 나타낼 수 있으며 이를 '절대값'이라고 부른다.
게임에서 어떠한 가상의 공간을 만들때 '수'는 그것을 구성하는 가장 작은 단위이다. 오늘은 수의 구조와 성질 그리고 수를 표현하는 방법 중 시각적인 선으로 표현하는 방법에 대해 알아보았다.
'Game Programming > 게임 수학' 카테고리의 다른 글
| [게임수학] 삼각함수 (0) | 2022.09.28 |
|---|---|
| [게임수학] 벡터 (0) | 2022.09.27 |
| [게임수학] 함수 (0) | 2022.09.21 |